Longest common subsequence problem

发表于   |   分类于 ， ，

The longest common subsequence (LCS) problem is the problem of finding the longest subsequence common to all sequences in a set of sequences (often just two sequences). It differs from problems of finding common substrings: unlike substrings, subsequences are not required to occupy consecutive positions within the original sequences. The longest common subsequence problem is a classic computer science problem, the basis of data comparison programs such as the diff utility, and has applications in bioinformatics. It is also widely used by revision control systems such as Git for reconciling multiple changes made to a revision-controlled collection of files. - - - - wikipedia

描述

最长公共子序列，所求得的字符串在原字符串中可以不连续

分析

动态规划思想，以一个二维数组来存储子串长度
由于可以不连续，所以在当前字符不匹配时，记录 Math.max(L[i - 1][j], L[i][j - 1]) ，而不是清零

流程：

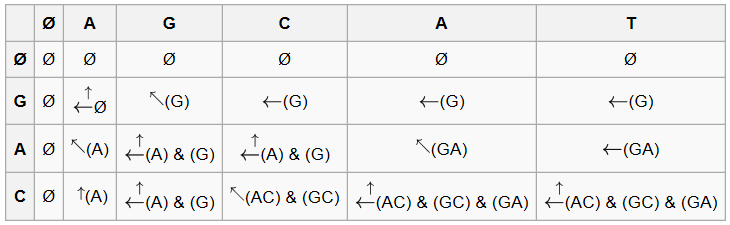
回溯：以长度来代替序列，生成二维数组之后，从 L[S.length() - 1][T.length() - 1] 开始回溯，输出 LCS（或 LCSs）

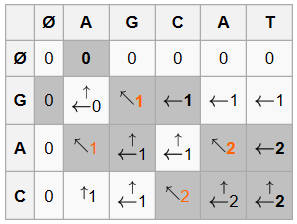
差异：通过回溯，还可以知道字符串之间的差异。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
import java.util.HashSet;
import java.util.Set;

public class Solution {

    private int[][] L = null;
    private String S;
    private String T;
    private Set<String> strings = null;

    Solution(String s, String t) {
        S = " " + s;
        T = " " + t;
    }

    public void setS(String s) {
        S = " " + s;
    }

    public void setT(String t) {
        T = " " + t;
    }

    public Set<String> getStrings() {
        return strings;
    }

    // Computing the length of the LCS
    public int LCSLength() {

        L = new int[S.length()][T.length()];

        for (int i = 1; i < S.length(); i++) {
            for (int j = 1; j < T.length(); j++) {

                if (S.charAt(i) == T.charAt(j)) {
                    L[i][j] = L[i - 1][j - 1] + 1;
                } else {
                    L[i][j] = Math.max(L[i - 1][j], L[i][j - 1]);
                }
            }
        }

        return L[S.length() - 1][T.length() - 1];
    }

    // Reading out an LCS
    public String readLCS() {

        LCSLength();
        return backtrack(S.length() - 1, T.length() - 1);
    }

    private String backtrack(int i, int j) {

        if (i == 0 || j == 0) {
            return "";
        }

        if (S.charAt(i) == T.charAt(j)) {
            return backtrack(i - 1, j - 1) + S.charAt(i);
        }

        if (L[i][j - 1] > L[i - 1][j]) {
            return backtrack(i, j - 1);
        }

        return backtrack(i - 1, j);
    }

    // Reading out all LCSs
    public void readLCSs() {

        LCSLength();
        strings = new HashSet<String>();

        backtrackAll(S.length() - 1, T.length() - 1, "");
    }

    private void backtrackAll(int i, int j, String lcs) {

        if (i == 0 || j == 0) {
            strings.add(lcs);
            return;
        }

        if (S.charAt(i) == T.charAt(j)) {
            backtrackAll(i - 1, j - 1, S.charAt(i) + lcs);
            return;
        }

        if (L[i][j - 1] >= L[i - 1][j]) {
            backtrackAll(i, j - 1, lcs);
        }

        if (L[i - 1][j] >= L[i][j - 1]) {
            backtrackAll(i - 1, j, lcs);
        }
    }

    // Print the diff
    public String diff() {

        LCSLength();
        return printDiff(S.length() - 1, T.length() - 1);
    }

    private String printDiff(int i, int j) {

        if (i > 0 && j > 0 && S.charAt(i) == T.charAt(j)) {
            return printDiff(i - 1, j - 1) + " " + S.charAt(i);
        }

        if (j > 0 && (i == 0 || L[i][j - 1] >= L[i - 1][j])) {
            return printDiff(i, j - 1) + " +" + T.charAt(j);
        }

        if (i > 0 && (j == 0 || L[i][j - 1] < L[i - 1][j])) {
            return printDiff(i - 1, j) + " -" + S.charAt(i);
        }

        return "";
    }
}