N-Queens

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle.

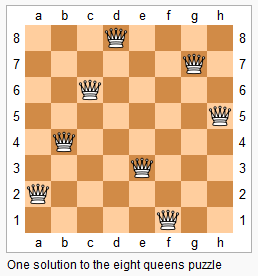
Each solution contains a distinct board configuration of the n-queens’ placement, where Q and . both indicate a queen and an empty space respectively.

描述

n 皇后问题，任意两个皇后都不能处于同一行、同一列或同一斜线上

分析

• 核心思想： 由于棋盘上每一行都只能放一个数，所以无需记录行的信息，这就便于将行折叠起来。这样整个棋盘便可以看成是一个二进制数，每个二进制位都是一列
• 注意： 回溯时，需要把棋盘的状态重置

代码

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class Solution {

    private char[][] board;  // 用来记录皇后放置状态
    private List<List<String>> lists;  // 用来存储返回的结果
    private long line; // n 位全部置为 1，用来判断是否已经将全部皇后放置完成

    public List<List<String>> solveNQueens(int n) {

        if (n == 0) {
            return lists;
        }

        lists = new ArrayList<List<String>>();
        board = new char[n][n];
        line = (1 << n) - 1;

        queens(0, 0, 0, 0);

        return lists;
    }

    // row 记录棋盘上已经放置的皇后的情况
    // ld 记录相邻左斜线的情况
    // rd 记录相邻右斜线的情况
    // ri 记录当前的行号
    private void queens(long row, long ld, long rd, int ri) {

        if (row != line) {      // 判断是否已放置完成

            long puts = line & (~(row | ld | rd));    // puts 记录当前允许放置的位置

            while (puts != 0) {

                long p = puts & (-puts);     // 取二进制形式下最右边的 1，表示为将要放置的位置
                puts -= p;

                int k = -1;    // 将放置的位置转换成棋盘上的列号
                long pp = p;
                while (pp != 0) {
                    pp >>= 1;
                    k++;
                }

                Arrays.fill(board[ri], '.');     // 回溯时，重置状态
                board[ri][k] = 'Q';

                queens(row + p, (ld + p) << 1, (rd + p) >> 1, ri + 1);
            }
        } else {

            lists.add(construct());
        }
    }

    // 将数组转换成 list
    private List<String> construct() {

        List<String> list = new ArrayList<String>();

        int n = board.length;
        for (int i = 0; i < n; i++) {
            String s = new String(board[i]);
            list.add(s);
        }

        return list;
    }
}