快速排序

发表于   |   分类于 ， ，

Quicksort is a divide and conquer algorithm. Quicksort first divides a large array into two smaller sub-arrays: the low elements and the high elements. Quicksort can then recursively sort the sub-arrays. - - - - wikipedia

The steps are:

  1. Pick an element, called a pivot, from the array.
  2. Partitioning: reorder the array so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
  3. Recursively apply the above steps to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values.

The base case of the recursion is arrays of size zero or one, which never need to be sorted.

The pivot selection and partitioning steps can be done in several different ways; the choice of specific implementation schemes greatly affects the algorithm’s performance.

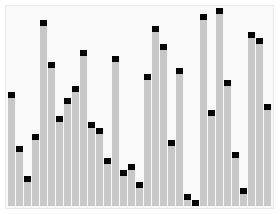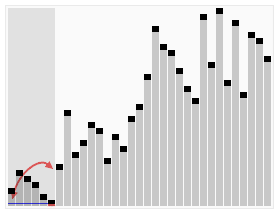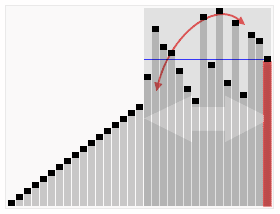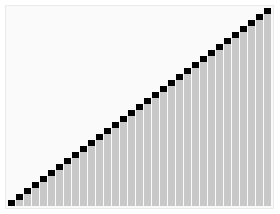
分析

快速排序的主要思想是，指定一个元素，通过这个元素，将区间分成两部分，左边不大于这个元素，右边不小于这个元素。再通过递归，将左右两边的区间不断划分，直至所有区间内都仅有一个元素，此时总区间已经有序

以 Hoare partition scheme 的方式来划分区间：使用两个标记 i，j，分别从左右两端向中间遍历，当 nums[i] 不小于指定元素 p（一般以区间的第一个数为指定元素）时停下，当 nums[j] 不大于 p 时停下，交换 nums[i] 和 nums[j]，之后继续遍历，直到 i >= j 时结束。此时区间已经被 p 划分成两块，左边元素不大于 p，右边元素不小于 p

特点

  • 不稳定的排序
  • 时间复杂度（最佳）： $O(n log(n))$
  • 时间复杂度（平均）： $O(n log(n))$
  • 时间复杂度（最差）： $O(n^2)$
  • 空间复杂度（最差）： $O(log(n))$ auxiliary

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
import java.util.Arrays;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {

        Scanner input = new Scanner(System.in);

        int n = input.nextInt();
        int[] nums = new int[n];

        for (int i = 0; i < n; i++) {
            nums[i] = input.nextInt();
        }

        quickSort(nums, 0, nums.length - 1);

        System.out.println(Arrays.toString(nums));
    }

    public static int partition(int nums[], int first, int last) {

        int pivot = nums[first];
        int i = first - 1;
        int j = last + 1;

        while (true) {

            do {
                i++;
            } while (nums[i] < pivot);

            do {
                j--;
            } while (nums[j] > pivot);

            if (i >= j) {
                return j;
            }

            int t = nums[i];
            nums[i] = nums[j];
            nums[j] = t;
        }
    }

    public static void quickSort(int nums[], int first, int last) {

        if (first < last) {
            int p = partition(nums, first, last);
            quickSort(nums, first, p);
            quickSort(nums, p + 1, last);
        }
    }
}

优化

  • 将指定元素随机产生，而不是取区间的第一个元素，这样可以尽量避免最坏情况的发生
  • 划分时返回两个值，left 和 right，这主要针对有大量重复值出现的情况
1
2
3
4
5
6
7
8
// pseudocode

algorithm quicksort(A, lo, hi) is
    if lo < hi then
        p := pivot(A, lo, hi)
        left, right := partition(A, p, lo, hi)  // note: multiple return values
        quicksort(A, lo, left)
        quicksort(A, right, hi)