归并排序

发表于   |   分类于 ， ，

Conceptually, a merge sort works as follows: - - - wikipedia

  1. Divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted).
  2. Repeatedly merge sublists to produce new sorted sublists until there is only 1 sublist remaining. This will be the sorted list.

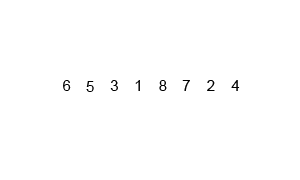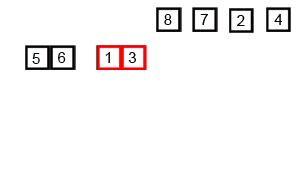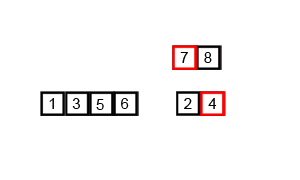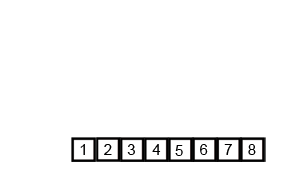
分析

采用自顶向下的方式，利用递归将列表分割成一个个子列表，直至所有的子列表的大小都为 1，然后再将左右相邻的子列表合并，直至所有的子列表都合并成一个列表。代码中采用 temp 数组来充当临时数组，存储子列表合并后的结果，再将其覆盖到原列表上

特点

  • 稳定的排序
  • 时间复杂度（最佳）： $O(n log(n))$
  • 时间复杂度（平均）： $O(n log(n))$
  • 时间复杂度（最差）： $O(n log(n))$
  • 空间复杂度（最差）： $O(n)$ auxiliary

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import java.util.Arrays;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {

        Scanner input = new Scanner(System.in);

        int n = input.nextInt();
        int[] nums = new int[n];

        for (int i = 0; i < n; i++) {
            nums[i] = input.nextInt();
        }

        mergeSort(nums, 0, nums.length - 1, new int[n]);

        System.out.println(Arrays.toString(nums));
    }

    public static void mergeArray(int nums[], int first, int mid, int last, int temp[]) {

        int i = first, m = mid;
        int j = mid + 1, n = last;
        int k = 0;

        while (i <= m && j <= n) {
            if (nums[i] <= nums[j]) {
                temp[k++] = nums[i++];
            } else {
                temp[k++] = nums[j++];
            }
        }

        while (i <= m) {
            temp[k++] = nums[i++];
        }

        while (j <= n) {
            temp[k++] = nums[j++];
        }

        for (i = 0; i < k; i++) {
            nums[first + i] = temp[i];
        }
    }

    public static void mergeSort(int nums[], int first, int last, int temp[]) {

        if (first < last) {

            int mid = (first + last) / 2;
            mergeSort(nums, first, mid, temp);
            mergeSort(nums, mid + 1, last, temp);
            mergeArray(nums, first, mid, last, temp);
        }
    }
}