Container with Most Water

Given n non-negative integers a1, a2, …, an, where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note:
You may not slant the container and n is at least 2.

描述

给定 n 个非负整数，每个数代表坐标上的一个点，每个点与 x 轴垂直画一条线，任选两条线与 x 轴组成一个容器，使容器能装的水最多。注意：容器不能倾斜

分析

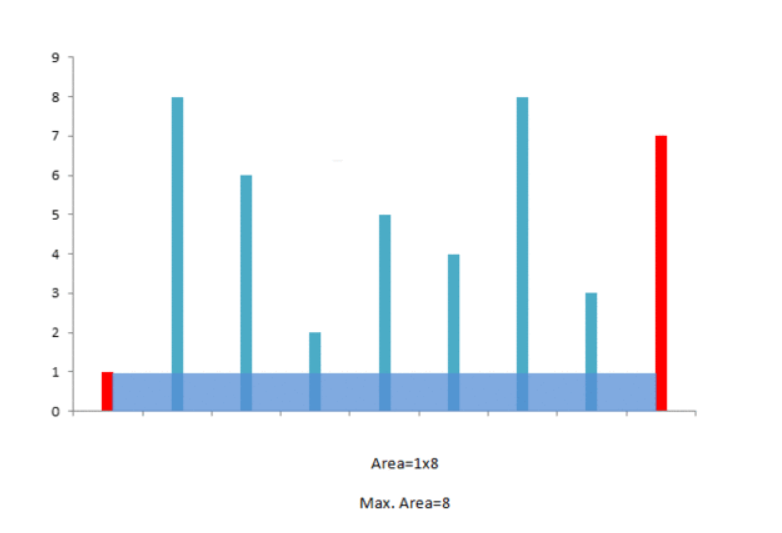
一个容器所能装的水取决于最短一边的高度，即 width * min(height[l] , height[r])，l 与 r 分别从两端开始，假设 height[l] < height[r]，那么当 r 向左移（向 l 靠近）时，最小高度不可能大于 height[l]，且 width 不断减少，所以 r 向左移没有判断的必要。只能 l 向右移（向 r 靠近），直到 height[l] >= height[r] 时，对象由 l 变成 r，重复此过程，直至 l 与 r 相遇

代码

public class Solution {
    public int maxArea(int[] height) {

        int max = 0, n = height.length;
        int l = 0, r = n - 1;

        while (l < r) {

            int h = Math.min(height[l], height[r]);
            int w = r - l;
            int area = h * w;

            if (max < area) {
                max = area;
            }

            if (height[l] < height[r]) {
                l++;
            } else {
                r--;
            }
        }

        return max;
    }
}